Home › International Fame

Understanding The Radical Mathematical Definition: A Comprehensive Guide

AuraInsider December 01, 2024

Mathematics is a vast field that encompasses various definitions and concepts, one of which is the radical mathematical definition. This definition is crucial for understanding how we manipulate and interpret expressions involving roots and powers. In this article, we will delve deep into the radical mathematical definition, its significance, and how it applies to different mathematical problems. By the end of this article, you will have a thorough understanding of this fundamental concept and its applications.

The radical mathematical definition provides a foundation for working with square roots, cube roots, and other higher-order roots. It is essential for students, educators, and anyone looking to brush up on their mathematical skills. We will explore the various aspects of radicals, including their properties, operations, and how they relate to equations. Whether you are a student preparing for an exam or a professional seeking to enhance your mathematical knowledge, this guide is designed to meet your needs.

As we navigate through this topic, we will also address common misconceptions and challenges associated with radicals. With clear explanations, practical examples, and relevant data, our aim is to equip you with the expertise and confidence to tackle problems involving radical expressions. So, let’s embark on this journey into the world of radical mathematics!

What are Radicals?
Definition and Properties of Radicals
Operations with Radicals
Simplifying Radicals
Radicals in Equations
Applications of Radicals
Common Misconceptions about Radicals
Conclusion

What are Radicals?

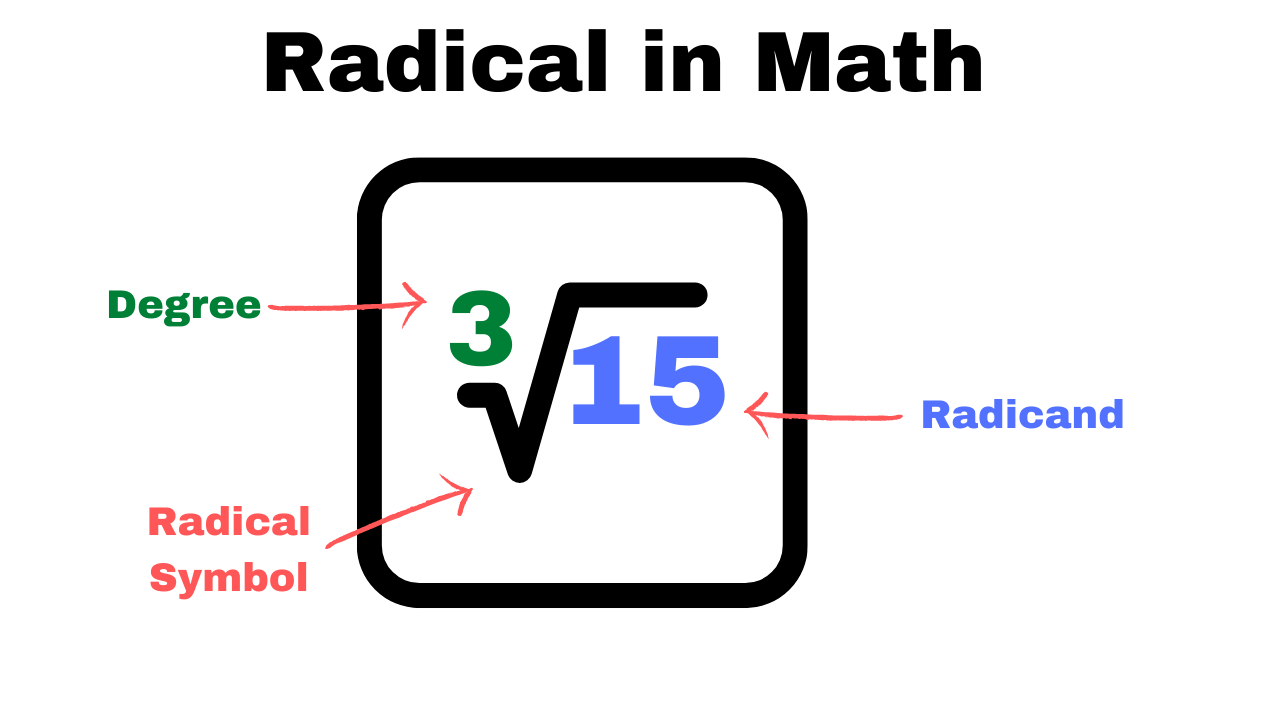
Radicals are mathematical expressions that involve roots, such as square roots, cube roots, and higher-order roots. The radical symbol (√) is used to denote these roots. For example, the square root of a number 'x' is expressed as √x, which represents the value that, when multiplied by itself, gives 'x'. Similarly, the cube root is denoted as ∛x, indicating the number that, when raised to the third power, results in 'x'.

Types of Radicals

Square Roots: The most common type of radical, denoted by √.
Cube Roots: Denoted by ∛, these involve finding a number that, when cubed, equals the radicand.
Higher-Order Roots: These include fourth roots, fifth roots, etc., denoted by corresponding radical symbols.

Definition and Properties of Radicals

The radical mathematical definition can be formally expressed as follows: a radical expression is an expression that includes a root. The general form of a radical expression is represented as:

√(a), ∛(b), or n√(c), where 'a', 'b', and 'c' are real numbers, and 'n' indicates the order of the root.

Key Properties of Radicals

Product Property: √(a) × √(b) = √(a × b)
Quotient Property: √(a) / √(b) = √(a / b)
Power Property: (√(a))^n = a^(n/2)

Operations with Radicals

Understanding how to perform operations with radicals is essential for manipulating radical expressions. The primary operations include addition, subtraction, multiplication, and division. Each operation has its own rules that must be followed.

Adding and Subtracting Radicals

When adding or subtracting radicals, the key is to combine like terms, similar to combining algebraic expressions. For example:

√2 + √2 = 2√2
3√5 - 2√5 = √5

Multiplying and Dividing Radicals

Multiplication and division of radicals follow the product and quotient properties mentioned earlier. For instance:

√3 × √12 = √(3 × 12) = √36 = 6
√50 / √2 = √(50 / 2) = √25 = 5

Simplifying Radicals

Simplifying radical expressions is crucial for making calculations easier. This involves eliminating perfect squares (or cubes, etc.) from within the radical. For example:

√18 can be simplified to √(9 × 2) = 3√2
√32 can be simplified to √(16 × 2) = 4√2

Radicals in Equations

Radicals often appear in equations, and solving these equations requires specific techniques. To eliminate the radical, one typically squares both sides of the equation. For example:

If √(x + 3) = 5, squaring both sides gives:

x + 3 = 25, so x = 22.

Applications of Radicals

Radicals have numerous applications in various fields, including physics, engineering, and statistics. Some examples include:

Calculating distances using the distance formula.
Solving problems involving area and volume where square and cube roots are applicable.
Statistical analysis, where standard deviation calculations often involve radicals.

Common Misconceptions about Radicals

Several misconceptions exist regarding radicals that can lead to confusion. Some of these include:

All radicals are irrational numbers: While many radicals are irrational (e.g., √2), some are rational (e.g., √4 = 2).
Simplifying a radical always results in an integer: This is not true, as radicals can remain in their simplified form.

Conclusion

In conclusion, the radical mathematical definition is an essential concept in mathematics, allowing us to work with roots and understand their properties and operations. By mastering the rules of radicals, simplifying expressions, and applying these concepts in equations, you can enhance your mathematical skills significantly. We encourage you to practice these principles regularly to solidify your understanding.

If you found this article helpful, please leave a comment below, share it with your friends, or explore more articles on our site!

References

Stewart, James. "Calculus: Early Transcendentals." Cengage Learning, 2015.
Blitzer, Robert. "Algebra and Trigonometry." Pearson, 2018.
Strang, Gilbert. "Linear Algebra and Its Applications." Cengage Learning, 2016.

Thank you for reading! We hope to see you back for more enlightening content.

Article Recommendations

Details